Éclairage sur la magnitude

L’éclat des étoiles se mesure en magnitude. Mais cette notion a des côtés déroutants pour le débutant, avec son échelle inversée et ses valeurs négatives… On vous explique tout !

Au début était la grandeur…

Au II^ème siècle avant J.-C., l’astronome grec Hipparque établit un premier classement des étoiles selon leur éclat apparent. Observant seulement à l’œil nu, il détermine six catégories d’intensités décroissantes, qu’il appelle grandeurs : une étoile très brillante est de première grandeur, une autre un peu moins lumineuse est de deuxième grandeur, ainsi de suite jusqu’à la sixième grandeur qui concerne les étoiles les plus faibles visibles à l’œil nu.

La première échelle pour mesurer l’éclat des étoiles s’étale donc de 1 à 6, du plus brillant au plus faible. Elle va servir pendant de nombreux siècles et être à la base du système actuel que l’astronome Norman Pogson établit en 1856.

… puis vint la magnitude

Car les grandeurs qu’Hipparque a déterminées de façon empirique restituent assez justement un fait transposable mathématiquement : la sensation d’éclat perçue par l’œil varie comme le logarithme de son excitation. Une propriété rigoureusement mise en équation par Norman Pogson dont découle l’échelle de magnitude, toujours en vigueur actuellement.

Pour l’exprimer simplement, un écart d’une magnitude correspond à une différence d’éclat de 2,512 : une étoile de magnitude 3 est donc 2,512 fois plus brillante qu’une étoile de magnitude 4.

Écart de magnitude entre deux astres	Rapport d’éclat
0,5	1,58
1	2,512
2	6,31
3	15,85
4	39,81
10	10 000

À l’époque de Norman Pogson, on dispose déjà d’instruments qui permettent de voir des objets invisibles à l’œil nu et l’échelle des magnitudes est donc étendue au-delà de 6. Par exemple, les plus faibles objets détectés par un télescope de 130 mm de diamètre ont une magnitude de 12,6. Mais Norman Pogson se rend également compte que Hipparque a sous-évalué l’éclat de certaines étoiles les plus brillantes. De plus, il souhaite aussi quantifier l’éclat d’astres encore plus lumineux : planètes, Lune, Soleil. Il décide donc d’étendre l’échelle de magnitude en deçà de 1 (on le rappelle encore, les étoiles de première grandeur d’Hipparque sont les plus brillantes), ce qui a pour conséquence d’attribuer des magnitudes de zéro ou de valeurs négatives.

On a donc maintenant tous les éléments pour comprendre l’échelle alambiquée des magnitudes :
une origine ancienne qui classe les étoiles en six grandeurs d’éclats, de la plus brillante à la plus faible, d’où les valeurs inversées ;
une extension de l’échelle dans sa forme moderne qui prend en compte des astres plus brillants, d’où l’apparition de valeurs négatives.

Quelles sont les magnitudes couramment rencontrées ?

La magnitude des différents astres observés depuis la Terre couvre donc désormais une large échelle. Voici quelques points de repère :

Objet	Magnitude
Soleil	-26,8
Lune (pleine lune)	-12,7
Planète Vénus (maximum)	-4,4
Planète Mars (maximum)	-2,8
Planète Jupiter (maximum)	-2,5
Sirius (étoile la plus brillante du ciel)	-1,5
Étoile Véga	0
Étoile Polaire	2
Planète naine Pluton	14
Grosses exoplanètes	28

Quelle magnitude puis-je atteindre avec mon instrument ?

Il est utile de connaître les capacités d’un instrument (jumelles, lunette, télescope…) pour savoir ce qu’il permet de voir et lequel choisir. On donne alors sa magnitude limite, valeur théorique indicative calculée à partir du diamètre instrumental, mais qui varie en fonction des conditions d’observation et de l’acuité visuelle de l’observateur. Voici quelques magnitudes limites théoriques :

Instrument	Magnitude limite
Œil nu	6
Jumelles de 50mm de diamètre	10
Lunette de 70 mm de diamètre	11,3
Télescope de 130 mm de diamètre	12,6
Télescope de 200 mm de diamètre	13,6
Télescope de 400 mm de diamètre	15,1
Télescope de 5 m de diamètre	20,6

Magnitude apparente et magnitude absolue

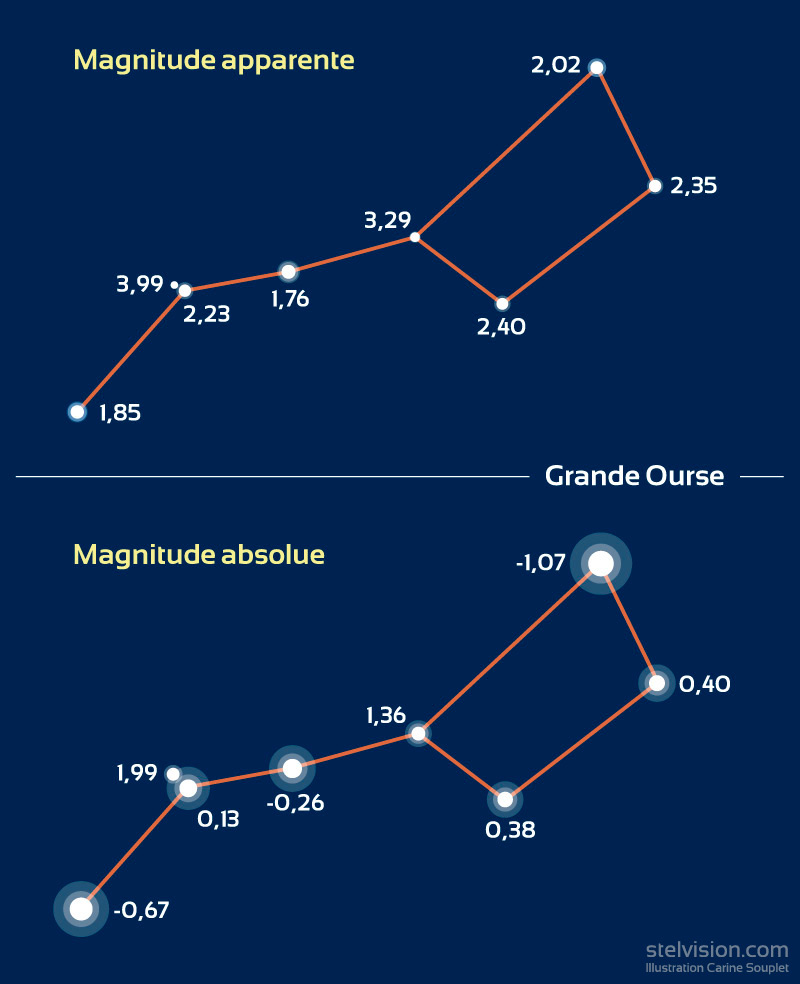
Jusque là, nous parlions de la magnitude des astres vus depuis la Terre, donc leur magnitude apparente. Mais les astronomes ont voulu rendre compte de l’éclat réel des étoiles les unes par rapport aux autres, comme si elles étaient toutes situées à la même distance (ce qui est très loin d’être le cas).

Ils ont donc calculé la magnitude absolue, qui correspond à l’éclat d’une étoile si elle était vue à 10 parsecs de distance (un parsec = 3,26 années-lumière). Par exemple, le Soleil dont la magnitude apparente est de -26,8 a une magnitude absolue de 4,8, tandis que l’étoile Antarès dont la magnitude apparente est de 1, a une magnitude absolue de -4,8.

La magnitude surfacique

Une autre notion souvent rencontrée en observation visuelle est celle de magnitude surfacique, appelée aussi brillance de surface : elle est utilisé pour les objets étendus et diffus (nébuleuses et galaxies notamment). En effet, la magnitude apparente d’un objet étendu donne une indication sur la totalité de la lumière qu’il émet, mais plus sa surface est grande et plus la lumière émise est répartie sur cette surface. Cela a pour conséquence qu’à magnitude apparente égale, plus un objet est grand et plus on a l’impression qu’il est faiblement lumineux.

Pour contourner cette difficulté, on a donc créé la magnitude surfacique qui donne l’éclat moyen de l’objet pour une portion de surface constante (l’unité est la magnitude par seconde d’arc au carré) et donne une idée plus juste de l’aspect visuel d’un objet étendu.

Magnitudes pour professionnels

Les photographes et scientifiques ont aussi leurs propres échelles de magnitude, qui englobent des portions variables du spectre lumineux des étoiles. La magnitude des astres dans les catalogues des astronomes professionnels est ainsi souvent éclatée en trois valeurs : une pour la magnitude correspondant à ce que l’œil perçoit (longueurs d’onde autour de 550 nm), une autre dans l’ultraviolet (autour de 360 nm) et une dernière dans le bleu (autour de 440 nm). Lorsque l’on donne ces mesures pour un astre, on parle de photométrie. Enfin la magnitude bolométrique donne quant à elle l’éclat d’un astre sur la totalité du spectre lumineux. On la mesure à l’aide d’un instrument spécifique appelé bolomètre.

Une mesure délicate

Avec une telle armada d’échelles, on se dit que l’éclat des astres est une grandeur qu’on connaît bien. Mais quelques éléments perturbateurs viennent pimenter les mesures ! Tout d’abord, celles effectuées depuis la Terre sont sujettes aux effets d’absorption variables de l’atmosphère. Et quand on mesure depuis l’espace, il faut savoir si des nuages de gaz ou de poussières ne se trouvent pas entre l’astre et nous ! Enfin, un grand nombre d’étoiles ont un éclat qui varie dans le temps. De quoi donner quelques sueurs froides à ceux qui établissent les catalogues stellaires !

Pour s’affranchir des perturbations de l’atmosphère, on s’appuie désormais sur d’ambitieuses missions spatiales chargées de mesurer avec précision les mensurations des étoiles, dont leur magnitude. Après Hipparcos en 1990, c’est la mission Gaia qui a répertorié près d’1,8 milliard d’objets célestes dans son catalogue définitif publié en 2022. De quoi avoir une source de données suffisamment vaste et précise pour quelques temps !